hedgehog lab Dev Challenge: Fibonacci Stairs — A JavaScript Solution

At the start of 2019 a ‘dev challenge’ was introduced here at hedgehog lab. The premise being that either fortnightly or weekly (depending on the complexity) a ‘challenge’ would be issued to the developers in our office‚ and we would then attempt to solve them‚ with a group meeting at the end of the week to go over all of our solutions.

The first challenge issued was definitely a tough one — we were presented with the following information;

A child is running up a staircase with n steps and can hop either 1 step‚ 2 steps‚ or 3 steps at a time. Implement a method to count how many possible ways the child can run up the stairs.

The challenge is to use recursion in order to calculate the number of possible ways the child can get up n number of stairs‚ hopping either 1‚ 2‚ or 3 at a time.

Recursion is a mathematical term which is defined as;

The repeated application of a recursive procedure or definition.

In summary‚ we need to repeat a method allowing us to calculate the amount of possible ways the child can get up an undefined amount of stairs.

Recursion was actually something I hadn’t come across as a developer before‚ which was the same for a large number of people in the office.

To begin with we need to assess the problem — let’s assume for the purpose of this exercise that our staircase has 4 stairs. Therefore‚ n = 4.

We know the child can hop up 1‚ 2‚ or 3 stairs at once‚ so with a staircase of 4 stairs the child can go up via any of these routes;

1–1–1–1‚
1–2–1‚
1–1–2‚
2–1–1‚
2–2‚
1–3‚
3–1.

In order to solve the problem we need to gather the information that we have;

• If there is a negative amount of steps there are no routes for the child to get up them as this scenario is impossible.
• If there are no steps or only one step there is only one way for the child to get up them — 1.
• We know the 3 possible ways the child can finish the steps. With 1‚ 2‚ or 3 steps.

This translates into a function which should look something like this;

countRoutes(stairs) {
    if (stairs < 0) {
        return 0;
    }

    if (stairs === 0) {
        return 1;
    }

    return this.countRoutes(stairs - 1) + this.countRoutes(stairs - 2) + this.countRoutes(stairs - 3);
}

So the solution to our problem comes from adding together the number of different ways the child can get up to our 3 finishing scenarios‚ hence — this.countRoutes(stairs – 1) + this.countRoutes(stairs – 2) + this.countRoutes(stairs – 3).

The concrete “base cases” of 0 or 1 steps serve as our exit clause‚ so we know when to stop the recursion.

So if n = 4 the number of possible ways the child can get up the stairs should equal 7.

Let’s break this function down and look at it in the form of recursion.

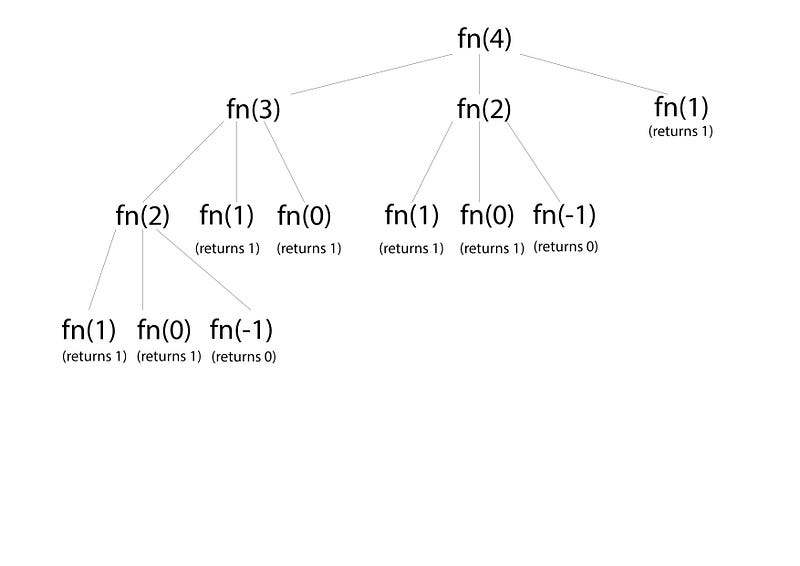
As we said before‚ we know the child can move up the steps in any of three ways‚ so if we have a staircase of 4 steps we need to take into account each of the ways the child can go up. So we break it down into 3 more loops of the function fn(4–1) (fn(3))‚ fn(4–2) (fn(2))‚ fn(4–3) (fn(1)).

For the third instance there’s only 1 step‚ we know there is only one way for the child to get up it‚ so we know the function will return 1.

For the other two instances we can break them down further. Essentially the tree will keep growing until each iteration of the function returns 1. We then add up all of the methods and as you can see from the above diagram —for 4 steps we end up with 7 possible routes.

Bonus Points — Memoization

However‚ there’s another issue to consider — call stack. Our recursion function can handle 4 stairs because the function will only run 13 times (see the above diagram). 13 iterations of a function is easy enough for the browser to handle. But‚ if we try and find the routes for 100 stairs‚ or more‚ we’re going to run into some issues in the browser.

That’s where memoization comes in — another new concept introduced with this challenge.

If you look at the above diagram again (ignore the instances of -1 and 0 because we return early for them without looping) there are 4 loops where n = 1‚ 2 loops where n = 2‚ 1 loop where n = 3‚ and 1 loop where n = 4. If we introduce memoization we can fix our function so that when n = 1 it will only loop once‚ and so on.

Memoization is defined as;

In computing‚ memoization or memoisation is an optimisation technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again.

In summary‚ we want to cache the results of each loop of the function in order to decrease the number of calls we have to make‚ so let’s add that to our function;

countRoutes(stairs‚ memory = {}) {
    if (stairs < 0) {
        return 0;
    }

    if (stairs === 0) {
        return 1;
    }

    if (memory[stairs]) {
        return memory[stairs];
    }

    return memory[stairs] = this.countRoutes(stairs - 1‚ memory) + this.countRoutes(stairs - 2‚ memory) + this.countRoutes(stairs - 3‚ memory);
}

And there you have it. The Fibonacci Stairs — a JavaScript solution. Surprisingly few lines of code for quite a complex problem.